▷ 작성자 : 붉은반점(r3dp0int@a3sc.co.kr)
▷ 편집자 : 니키 (ngnicky@a3sc.co.kr)
I. 분석보고서에 대한 소개
1. 목적
ARIA는 전자정부 구현을 위해 개발되고 최근에 소스코드를 홈페이지에 공개한 ARIA 암호 알고리즘에 대해 공부해보고 그 원리에 대한 이해를 돕기 위해 명세서와 소스코드를 나름대로의 논리로 정리해 보았습니다. 본 문서는 전자도서관 등에서 구할 수 있는 논문이나 현재 공개되어 있는 소스코드, 명세서, 벡터코드 등의 자료들을 참고하여 새로운 창조물이 아닌 현재 나온 자료에 대한 나름대로의 정리자료라고 할 수 있겠습니다
현재 완성된 보고서의 내용은 수학적인 부분을 중심으로 어떻게 알고리즘이 구성되었는가 의 내용입니다. 100% 이해한 내용이 아니므로 미숙한 내용이 있더라도 이해해주시기 바랍니다.
II. ARIA 암호알고리즘의 소개
1. 소개
ARIA는 전자정부 구현 등으로 다양한 환경에 적합한 암호 알고리즘이 필요함에 따라 국가보안기술연구소(NSRI) 주도로, 학계, 국가정보원 등의 암호기술 전문가들이 힘을 모아 개발한 국가 암호화 알고리즘입니다.
ARIA는 경량 환경 및 하드웨어 구현을 위해 최적화된, Involutional SPN 구조를 갖는 범용 블록 암호 알고리즘입니다. ARIA의 주요 특성은 다음과 같습니다.
블록 크기 : 128비트
키 크기 : 128/192/256비트 (AES와 동일 규격)
전체 구조: Involutional Substitution-Permutation Network
라운드 수 : 12/14/16 (키 크기에 따라 결정됨)
ARIA는 경량 환경 및 하드웨어에서의 효율성 향상을 위해 개발되었으며, ARIA가 사용하는 대부분의 연산은 XOR과 같은 단순한 바이트 단위 연산으로 구성되어 있습니다. ARIA라는 이름은 Academy(학계), Research Institute(연구소), Agency(정부 기관)의 첫 글자들을 딴 것으로, ARIA 개발에 참여한 학•연•관의 공동 노력을 표현하고 있습니다.
ARIA는 2004년 12월 30일에 한국산업규격 KS표준으로 제정되었으며 소스코드, 명세서 등의 자료들은 현재 국가사이버안전센터 IT인증사무국 홈페이지에서 배포하고 있습니다.
2. SEED와 차이점
|
|
ARIA |
SEED |
|
표준화 |
기술표준원에서 제정 |
정보통신단체표준(TTA)제정 IETF 표준으로 제정, ISO/IEC 국제블록암호알고리즘 표준으로 제정 |
|
키 길이 |
128비트 고정적 |
128, 196, 256비트 가변적 |
|
알고리즘 구조 |
Feistal 구조 |
SPN 구조 |
|
성능차이 |
ARIA : SEED 암호화 시간 비율 = 1 : 2 (성능 면에서 ARIA가 우수) | |
III. ARIA 알고리즘의 구조
1. 개요
ARIA는 대치, 확산, 키 적용 단계를 반복하는 SPN 구조로써 대치 단계에서는 S-box를 이용하여 바이트 단위로 치환을 하고, 확산 단계에서는 16X16 Involution 이진 행렬을 사용한 바이트 간의 확산을 한다.
n라운드 암호화와 복호화 과정은 최초의 키(eK1)를 적용한 후에 S-box 대치, 확산 , 키 적용 단계를 n-1 라운드 반복한 이후 최종 단계 n라운드에서는 S-box 치환과 키 적용 단계로만 구성을 하고 있습니다. (이유: 암호화와 복호화를 동일하게 하기 위해)
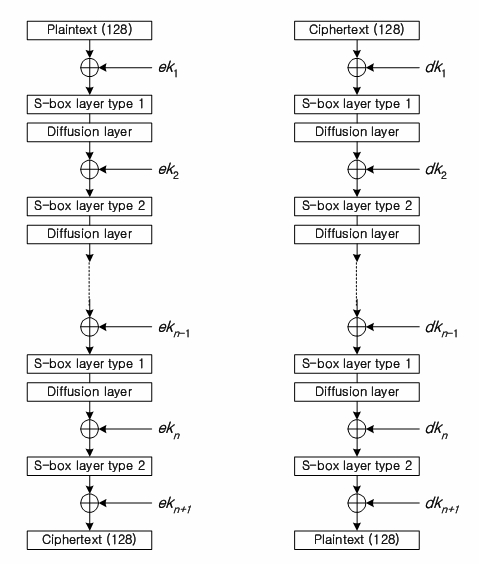
[그림 1] ARIA 암호화와 복호화 과정
2. 세부사항
1) 치환 계층(SubstLayer)
두 유형의 치환 계층이 있으며, 각각은 2종의 8비트 입출력 S-box와 그들의 역변환(reverse)로 구성됩니다.
S-box에 요구되는 성질
i. 최대 차분 / 선형 확률 : 2-6
ii. 대수적 차수 : 7
iii. 고정점, 반고정점이 없을 것.
일반적으로 이 같은 성질을 만족시키기 위하여 유한체 GF(28)상의 함수 x-1에 아핀변환(affine Transformation)을 사용하고 있습니다.
S-box S1,S2는 아래의 식이 성립:
S1 = Bx-1 XOR b // S2 = Cx247 XOR c
B,C는 8x8 정칙행렬이고, b,c는 8x1 행렬입니다.
S-box에서는 S1,S2와 함께 S1-1,S2-1을 사용하여 총 4개의 S-box를 사용합니다.
S1과 S1-1, S2와 S2-1은 서로 역의 관계입니다.
S-box는 32비트 단위를 사용.
2) 확산 계층(Diffusion Layer)
간단한 16 x 16 involution 이진 행렬을 사용한 바이트 간의 확산 함수로 구성되어 있습니다.
ARIA의 확산함수
A : GF(28)16 GF(28)16
입력 : (x0,x1,….,x15)
출력 : (y0,y1,….,y15)
16 x 16 이진행렬의 곱으로 표현
A는 A-1 = A로써 Involution 구조. 입력(y0,y1,y2,…..,y15) 출력(x0,x1,….,x15)가 가능.
가지수 β(A) = 8 = min{wt(x) + wt(Ax) | x∈ GF(28)16, x≠0} (단, wt(x) = x의 Hamming weight(‘x’에 포함된 ‘0’이 아닌 바이트 수))
3) 키 확장(Key Expansion, AddRoundKey)
초기화 과정에서는 암/복호화 한 라운드를 F함수로 하는 256비트 입출력 3라운드 Feistel 암호를 이용하여, 암호키 MK로부터 4 개의 128비트 값 W0,W1,W2,W3를 생성합니다. MK의 길이는 128, 192, 256가 가능하므로 Feistel 암호의 입력에 필요한 256비트(KL,KR)을 다음과 같이 구성합니다.
128비트 KL은 MK의 상위 128비트를 취합니다.
MK의 남은 비트를 이용하여 KR의 상위 비트를 채우고 나머지는 0으로 채웁니다.
KL || KR = MK || 0….0 >> MK가 128비트인 경우
KL || KR = MK(128) || (129~192),0….0 >> MK가 192비트인 경우
FO와 Fe를 각각 홀수(LT)와 짝수(LT-1)라운드 함수라고 할 때, W0,W1,W2,W3 은 다음의 공식으로 생성합니다.
W0 = KL
W1 = FO(W0,CK1) XOR KR
W2 = Fe(W1,CK2) XOR W0
W3 = FO(W2,CK3) XOR W1
Feistel 암호의 128비트 라운드 키 CKi는 π-1의 유리수 부분의 128비트 상수
C1 = 0x517cc1b727220a94fe13abe8fa9a6ee0
C2 = 0x6db14acc9e21c820ff28b1d5ef5de2b0
C3 = 0xdb92371d2126e9700324977504e8c90e
|
암호키 길이 |
CK1 |
CK2 |
CK3 |
|
128-비트 |
C1 |
C2 |
C3 |
|
192-비트 |
C3 |
C1 |
C2 |
|
256-비트 |
C2 |
C3 |
C1 |
라운드 키 생성과정
위에서 나온 값들을 이용하여 암호화와 복호화 라운드 키(eki, dki)를 생성합니다.
라운드 수는 x비트일 경우 (x+256)/32 라운드 수. (각각 12,14,16 라운드)
마지막 라운드에 키 덧셈 계층이 두 번 있으므로 13,15,17 개의 라운드 키 생성.
라운드 암호화 키 생성 공식
ek1 = (W0) XOR (W1>>>19), ek2 = (W1) XOR (W2>>>19)
ek3 = (W2) XOR (W3>>>19), ek4 = (W3) XOR (W0>>>19)
ek5 = (W0) XOR (W1>>>31), ek6 = (W1) XOR (W2>>>31)
ek7 = (W2) XOR (W3>>>31), ek8 = (W3) XOR (W0>>>31)
ek9 = (W0) XOR (W1>>>61), ek10 = (W1) XOR (W2>>>61)
ek11 = (W2) XOR (W3>>>61), ek12 = (W3) XOR (W0>>>61)
ek13 = (W0) XOR (W1>>>31), ek14 = (W1) XOR (W2>>>31)
ek15 = (W2) XOR (W3>>>31), ek16 = (W3) XOR (W0>>>31)
ek17 = (W2) XOR (W3>>>19)
복호화 라운드 키 생성 공식
dk1 = ekn+1, dk2 = A(ekn), dk3 = A(ekn-1), …. , dkn = A(ek2), dkn+1 = ek1
3. 소스코드 분석
현재 국가보안기술연구소 홈페이지에 공개되어 있는 소스는 테스트 용도로써 치환, 확산, 키 확장 등의 원리를 이해하는데 도움이 되었으며, 본 소스코드 암호화 이후의 결과가 정상적으로 이루어지는가와 암호화 복호화가 잘 이루어 지는가에 대한 확인을 그 목적으로 하고 있습니다.
1) 중요 함수
확산 계층 함수, 암호화 키 생성 함수, 복호화 키 생성 함수, 라운드 키 생성함수, 치환 및 암호화 함수
2) 확산 계층 함수 – DL(const Byte *i, Byte *o)
확산 계층 함수 : DL함수(FO, Fe 부분을 담당)
입력값 : input 배열과 output 배열 선언 >> DL(const Byte *I, Byte *O)
확산과정을 거치기 위한 임의의 공간 T 선언 >> Byte T;
일정한 규칙에 따른 4개의 인자 값을 XOR 계산
출력값 output 배열에 T값과 해당되는 인자 값에 키 값과 XOR 한 값을 저장합니다.
소스코드 일부분:
T = i[ 3] ^ i[ 4] ^ i[ 9] ^ i[14]; // T 값에 XOR 결과값 입력
o[ 0] = i[ 6] ^ i[ 8] ^ i[13] ^ T; // T와 각각의 output 값 생성
o[ 5] = i[ 1] ^ i[10] ^ i[15] ^ T;
o[11] = i[ 2] ^ i[ 7] ^ i[12] ^ T;
o[14] = i[ 0] ^ i[ 5] ^ i[11] ^ T;
3) 암호화 키 생성 함수 – EncKeySetup(const Byte *w0, Byte *e, int keyBits)
입력값은 첫번째 라운드 키 w0, 암호화된 라운드 키 e, 키 비트 KeyBits
임시 저장장소 t[16], 라운드 키 w1[16], w2[16], w3[16]
q = Fesitel 암호 라운드 키 세가지 구분(0 = C1, 1 = C2, 2 = C3)
int EncKeySetup(const Byte *w0, Byte *e, int keyBits) {
int i, R=(keyBits+256)/32, q;
Byte t[16], w1[16], w2[16], w3[16];
q = (keyBits - 128) / 64; // Feistel 암호 라운드 키 C1=0, C2=1, C3=2
for (i = 0; i < 16; i++) t[i] = S[ i % 4][KRK[q][i ] ^ w0[i]];
// S-box 에서 x값은 S-box s1,s2,s1-1,s2-1 4가지가 한번씩 돌아가면서 입력되도록 체크
// KRK[q][i]^w0[i] Feistel 암호 라운드 키와 암호화 라운드 키를 한 비트씩 XOR 연산
DL (t, w1); // 확산함수를 통한 w1값 결정
if (R==14)
for (i = 0; i < 8; i++) w1[i] ^= w0[16+i];
else if (R==16)
for (i = 0; i < 16; i++) w1[i] ^= w0[16+i];
q = (q==2)? 0 : (q+1);
for (i = 0; i < 16; i++) t[i] = S[(2 + i) % 4][KRK[q][i] ^ w1[i]];
DL (t, w2); // 확산함수를 통한 w2 결정
for (i = 0; i < 16; i++) w2[i] ^= w0[i]; //w2와 w0 XOR 연산
q = (q==2)? 0 : (q+1);
// Feistel 암호화 라운드 키를 키 비트수에 따라 하나씩 밀려서 쓰기 때문에 이와 같은 방법을 선택. 2가 되면 0으로 돌리고, 2가 되기 전까지는 +1 을 함.
for (i = 0; i < 16; i++) t[i] = S[ i % 4][KRK[q][i] ^ w2[i]];
DL (t, w3); //
for (i = 0; i < 16; i++) w3[i] ^= w1[i];
for (i = 0; i < 16*(R+1); i++) e[i] = 0; //e[i] 값을 초기화
아래의 RotXOR 함수는 아래에서 따로 설명하겠습니다.
RotXOR (w0, 0, e ); RotXOR (w1, 19, e );
RotXOR (w1, 0, e + 16); RotXOR (w2, 19, e + 16);
RotXOR (w2, 0, e + 32); RotXOR (w3, 19, e + 32);
RotXOR (w3, 0, e + 48); RotXOR (w0, 19, e + 48);
RotXOR (w0, 0, e + 64); RotXOR (w1, 31, e + 64);
RotXOR (w1, 0, e + 80); RotXOR (w2, 31, e + 80);
RotXOR (w2, 0, e + 96); RotXOR (w3, 31, e + 96);
RotXOR (w3, 0, e + 112); RotXOR (w0, 31, e + 112);
RotXOR (w0, 0, e + 128); RotXOR (w1, 67, e + 128);
RotXOR (w1, 0, e + 144); RotXOR (w2, 67, e + 144);
RotXOR (w2, 0, e + 160); RotXOR (w3, 67, e + 160);
RotXOR (w3, 0, e + 176); RotXOR (w0, 67, e + 176);
RotXOR (w0, 0, e + 192); RotXOR (w1, 97, e + 192);
if (R > 12) {
RotXOR (w1, 0, e + 208); RotXOR (w2, 97, e + 208);
RotXOR (w2, 0, e + 224); RotXOR (w3, 97, e + 224);
}
if (R > 14) {
RotXOR (w3, 0, e + 240); RotXOR (w0, 97, e + 240);
RotXOR (w0, 0, e + 256); RotXOR (w1, 109, e + 256);
}
return R;
}
4) 복호화 키 생성 함수 – DecKeySetup(const Byte *w0, Byte *d, int keyBits)
w0 : 암호화 라운드 첫번째 값, d : 복호화 라운드 키, KeyBits : 키 비트 수
int DecKeySetup(const Byte *w0, Byte *d, int keyBits) {
int i, j, R;
Byte t[16];
R=EncKeySetup(w0, d, keyBits); // 암호화 라운드 키 생성
// d값에는 암호화된 라운드 키가 입력되어 있음.
for (j = 0; j < 16; j++){
t[j] = d[j];
d[j] = d[16*R + j]; // 암호화된 라운드 키를 치환하는 부분
d[16*R + j] = t[j];
// 치환을 통한 복호화 라운드 키 생성
}
for (i = 1; i <= R/2; i++){
DL (d + i*16, t);
DL (d + (R-i)*16, d + i*16);
for (j = 0; j < 16; j++) d[(R-i)*16 + j] = t[j];
}
// 확산 및 치환 단계를 처리하는 부분
return R;
}
5) 라운드 키 생성 함수 – RotXOR(const Byte *s, int n, Byte *t)
s : 라운드 키로 얻은 네, 개의 비트 값, n : 쉬프트 비트 수, 암호화 키 배열 eKi값
void RotXOR (const Byte *s, int n, Byte *t)
{
int i, q;
q = n/8; n %= 8;
for (i = 0; i < 16; i++) {
t[(q+i) % 16] ^= (s[i] >> n);
if (n != 0) t[(q+i+1) % 16] ^= (s[i] << (8-n));
}
// 두 가지 경우의 수로 나누어서 비트 쉬프트 연산과 XOR 연산 수행
}
6) 치환 및 암호화 함수 – Crypt(const Byte *p, int R, const Byte *e, Byte *c)
P : 평문 바이너리, R : 라운드 수, e :
void Crypt(const Byte *p, int R, const Byte *e, Byte *c)
{
int i, j;
Byte t[16];
for (j = 0; j < 16; j++) c[j] = p[j];
for (i = 0; i < R/2; i++) // 라운드의 절반만 루프를 돌린다 하지만 내부에 두 번씩(S라는 함수와 역함수S-1 교대로) 돌게 되어있음.
{
for (j = 0; j < 16; j++) t[j] = S[ j % 4][e[j] ^ c[j]];
DL(t, c); e += 16;
for (j = 0; j < 16; j++) t[j] = S[(2 + j) % 4][e[j] ^ c[j]];
// S-box 교대로 적용하기 위해 +2가 적용됨. 나머지는 같음.
DL(t, c); e += 16;
}
DL(c, t);
for (j = 0; j < 16; j++) c[j] = e[j] ^ t[j]; // 최종 라운드에서 한번 더 ekn+1 키 교환
}
IV. 마무리
1. 끝맺으며
ARIA 알고리즘을 분석해보겠다고 덥썩 덤벼들긴 했지만, 수학적인 능력과 암호학에 대한 이해, 분석을 위해 주어진 시간(이 부분은 능력에 비례하는 것일지도 모르겠다.)이 부족하여 결국에는 알고리즘에 대한 소개와 명세어의 요약정도에 그친 것 같아 아쉬웠습니다. 블로그들을 검색해보니 이보다 더 훌륭한 글들이 많아서 오픈해야 하나 참 많이 망설였습니다.
실제 우리 주변에서 SEED와 함께 쓰일 암호 알고리즘으로써 정부기관을 축으로 사용될 것으로 예측되고, 여러 학회에서 발표된 자료에 안전성이 어느정도는 입증(SEED보다 안전?)된 것도 같습니다. 실제로 이 부분에 대한 증명에 관한 자료도 존재하였습니다. 향후에, 이 부분에 대한 증명을 스스로 해보고 싶은 욕구도 생기더군요.
부족한 글이지만, 여기까지 읽어주셨다면 감사하다고 말씀드리고 싶네요. 읽으시느라 수고하셨습니다.
2. 참고문헌
1) 안전성과 효율성을 갖춘 128-비트 블록 암호 알고리즘 설계 및 분석 /임웅택 – 국회전자도서관 / 서울 : 숭실대 대학원, 200502
※참고한 내용 : ARIA 에 대한 소개 글에 포함된 그림 사용.
2) ARIA 명세서 및 소스코드 공개 : 국가정보원 IT 보안인증사무국 페이지 :
http://www.kecs.go.kr/pw_certified/aria_open.jsp
3. 용어설명
1) ARIA : Academy, Research Institute, Agency 의 약어. 학연관이 공동으로 개발함을 함축.
2) Involution 구조 : 암호화 과정과 복호화 과정이 같은 구조
3) S-box : 비선형 치환 테이블로 바이트 치환에 사용됨.
4) SPN 구조 : Substitute-Permutation-Network 구조로 S-box와 확산 함수가 반복적으로 사용되는 구조
5) Feistel 구조 : 데이터를 두 블록으로 나누어 좌우 부분에 교대로 비선형 변환을 적용시키는 구조.
6) 대칭키 암호 : 암복호화 키가 같은 암호
7) 라운드 키 : 암호키로부터 키 확장을 통하여 생성되는 값들로 암호화 및 복호화 상태에 적용됨.
8) 라운드 함수 : 블록 암호의 각 라운드에서 사용되는 함수
9) 복호화 : 암호키를 이용하여 암호문을 평문으로 바꾸는 일련의 변환들
10) 블록 : 입력, 상태, 출력, 라운드 키를 구성하는 비트 열로 열의 길이는 포함하는 비트 수를 표시, 블록은 바이트의 배열로도 해석 가능.
11) 블록 암호 : 고정된 길이의 평문 블록을 고정된 길이의 암호문 블록으로 변환하는 함수
12 ) 상태 (state) : 암호화, 복호화 과정의 중간 값
13) 아핀 변환(Affine Transformation) : 행렬의 곱과 벡터의 합이 순차적으로 구성된 변환
14) 키 확장 : 암호 키로부터 라운드 키들을 생성하는 과정
15) MK : 암호 키
16) XOR : 배타적 논리합 연산
17) A <<< k : A의 각 비트를 왼쪽으로 k비트씩 순환이동.
18) A >>> k : A의 각 비트를 오른쪽으로 k비트씩 순환이동.